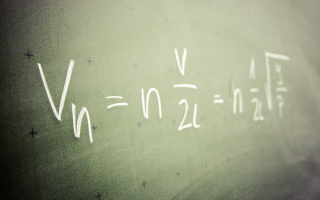2023考研數學一真題及答解析1

1、答：C 解析：函數有界性：函數既有上界又有下界，則稱之為有界函數。微分方程類型：微分方程 $y + ay + by = 0$ 是齊次線性微分方程。解的三種情況：第一種情況：$a^2 - 4b 0$，$lambda_1 neq lambda_2$。此時，$lambda_1$ 和 $lambda_2$ 至少有一個不等于零。

2、曲線的斜漸近線方程為。【解析】通過計算得知，該曲線只有一條斜漸近線，方程為。【注1】表示公式解釋，曲線只有一條漸近線。【注2】表示采用洛必達法則進行求解。

3、對于2023年考研數學一真題中分塊矩陣秩的比較問題，正確答為B，即（r_1 leq r_3 leq r_2）。 以下為具體分析： 分析（r_1）的取值范圍已知矩陣（M_1 = begin{pmatrix}O & A B & Cend{pmatrix}），根據分塊矩陣的初等變換性質，對（M_1）進行初等變換。

4、課程涵蓋：1987——2021年歷年真題及真題答解析，全面無償供同學們。PART 01打開賽氪，點擊課程一欄。PART 02選擇考研數學競賽課程。

5、考研數學一每年的平均分情況如下：2023年數學一平均分約為60.7分，年約為50.3分，2024年平均分預計在60至70分之間，2025年平均分同樣預計在60至70分之間，但部分高分考生可能達到90分以上。平均分波動原因數學一的平均分受題目難度影響顯著。

2023考研數學一真題及答解析

1、答：C 解析：函數有界性：函數既有上界又有下界，則稱之為有界函數。微分方程類型：微分方程 $y + ay + by = 0$ 是齊次線性微分方程。解的三種情況：第一種情況：$a^2 - 4b 0$，$lambda_1 neq lambda_2$。此時，$lambda_1$ 和 $lambda_2$ 至少有一個不等于零。

2、曲線的斜漸近線方程為。【解析】通過計算得知，該曲線只有一條斜漸近線，方程為。【注1】表示公式解釋，曲線只有一條漸近線。【注2】表示采用洛必達法則進行求解。

3、對于2023年考研數學一真題中分塊矩陣秩的比較問題，正確答為B，即（r_1 leq r_3 leq r_2）。 以下為具體分析： 分析（r_1）的取值范圍已知矩陣（M_1 = begin{pmatrix}O & A B & Cend{pmatrix}），根據分塊矩陣的初等變換性質，對（M_1）進行初等變換。

4、課程涵蓋：1987——2021年歷年真題及真題答解析，全面無償供同學們。PART 01打開賽氪，點擊課程一欄。PART 02選擇考研數學競賽課程。

2021考研數學一真題+答解析(完整版)

選擇題：考生需從四個選項中選出一個正確答。 若函數f（x）在區間[a，b]上連續，則下列說確的是（A）f（x）在區間[a，b]上有最大值與最小值；（B）f（x）在區間[a，b]上必有極值點；（C）f（x）在區間[a，b]上必有零點；（D）f（x）在區間[a，b]上單調遞增。解析：正確答為（A）。

年全國碩士研究生招生考試數學一試題解析 本題是一道常規分段函數臨界點可導性的斷問題，分段函數臨界點的可導性斷是一元微分學的重點，但斷方法唯一，即利用臨界點的導數定義。《新金講》在第二章中的重難點專題中有重點解析，本題與書中例27本質一致。

云逸未來將在12月28日（周一）晚20：00點，舉辦一場《21考研難度分析及線預測》交流分享會，為21/22考研學子提供直播服務，內容涵蓋21考研各難度、線各專業漲跌趨勢、今年擴招趨勢、21復試準備及22初試籌備等事宜。

基礎階段（2月底-5月底）時間分配：每日4小時數學學習，重點夯實基礎。學習資料：高數：張宇《基礎三十講》+ B站視頻課。線代與概率論：李永樂、王式安《復習全書》（自學，未跟視頻）。學習方式：基礎知識學習兩遍，確保無遺漏。刷題以教材例題為主，未額外拓展題量。

考研數學12年真題21題為什么r(ATA)=r(A)呢?

1、那么n-r（ATA）=n-r（A）6）證明結束 可能有些人對第四步有疑問，說AX不等于零，如果不等于零，AX是一個列向量，前面是他的行向量，這個乘積是AX的模，就不可能等于零了，所以AX必須等于零向量。

2、R（ATA） = min（R（AT） + R（A） = n所以R（A）=R（ATA） victor0o0 | 發布于2009-11-09 | 評論（4） 4 20 如果你知道奇異值分解，那么結論顯然。如果不知道就這樣做：若r（A）=k，那么可以用Gauss消去法把A消成梯陣，即CA=U，其中C是行初等變換的乘積，U僅有前k行非零且線性無關。

3、抽樣信號也被稱為抽樣函數或Sa（t）函數，是指sint與t之比構成的函數。抽樣信號是指正弦函數和自變量之比構成的函數，其表達式為：抽樣函數是一個偶函數，在t的正、負兩方向振幅都逐漸衰減，當t =π，2π，3π...，nπ時，函數值等于零。